Estructuras Delgadas
|
El análisis de estructuras delgadas es fascinante dado que aparte de ofrecer desafíos científicos en ciencia básica además permite acceder a ámbitos tan diferentes como el de la biología, medicina, ingeniería e incluso el arte. Por dar un ejemplo, en nuestro cuerpo podemos observar su importancia en los recubrimientos dado por la piel, todos los tubos internos como arterias, venas esófago, bronquios, alveolos y en general todas las estructuras separando dos medios en nuestro organismo. Los intereses en investigación del laboratorio abarcan diferentes areas entre las cuales están:
Estos problemas se estudian tanto desde el punto de vista experimental como también por medio de simulaciones numéricas y teoría. |
|
|
CrumplingCuando una superficie se deforma existen dos energías dominantes, una de doblamiento y otra de estiramiento. El hecho que la energía de doblamiento es proporcional al espesor de la película h al cubo y la energía de estiramiento es proporcional al espesor implica que la energía total de una superficie se puede escribir como Energía Mecánica=h3 (doblamiento)+h (estiramiento) Por tanto al deformar es mas barato doblar que estirar cuando el espesor es mas y mas pequeños. Esto trae una serie de consecuencias geométricas como la invariancia de longitudes a lo largo de la superficie, conservación de la curvatura gaussiana, aparición de singularidades, líneas y puntos, conectando dos regiones, etc. Dos de las estructuras básicas es un pliegue con curvatura gaussiana negativa conectando dos planos estudiada por T.A. Witten y H. Li (Europhysics Letters, 23, 51-55, 1993) y que aparece no sólo en problemas de "crumpling" sino también en diversas situaciones. Una segunda estructura es la aparición de singularidades cónicas las cuales han sido denominadas d-conos (M. Ben Amar and Y. Pomeau, Proc. R. Soc. London A, 453, 729-755, 1993) y que fueron estudiadas en detalle por nosotros posteriormente. |
|
|
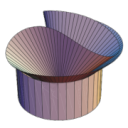
FoldingBajo grandes deformaciones inextensibles (o isométricas) se producen diversos fenómenos interesantes que pueden ser definidas por la palabra "folding". Este tipo de deformación se puede describir en el plano (2D) o en el espacio (3D) bajo la restricción que la curvatura gaussiana de la superficie se mantiene constante. Un ejemplo es cuando se enrolla una superficie o filamento ("coiling") lo cual es una forma de reducción en tamaño aunque no en volumen. Otra aplicación que hemos estudiado es la deformación de granos de polen. Estos tienen una cubierta rígida llamada exina y una región blanda llamada intina que cubre los orificios de la exina. Estos orificios son verdaderas articulaciones que le permiten a los granos de polen cerrarse o abrirse dependiendo de las condiciones de humedad. Hemos demostrado que el mecanismo de abertura y cerrado se puede predecir utilizando la condición de conservación de la curvatura gaussiana. Mas aún, la gran variedad de granos de polen permiten suponer que existen nuevas formas de deformar isométricamente de forma de cerrar una abertura. |
|
|
WrinklingTensión uniaxial pueden producir un estado muy lejos de la condición de "buckling" o primera inestabilidad, que queda marcado por el plegamiento o "wrinkling" de la superficie. Bajo este estado el esfuerzo en la dirección perpendicular a la tensión es prácticamente nula pero levemente compresivo. Este estado fue primero estudiado por Wagner quién mostró que corresponde a un estado muy lejos de condiciones de buckling donde también hay plegamiento pero de diferentes características. Bajo el supuesto de Wagner de tener un estado colapsado es posible describir la macroestructura del plegado de una superficie (largo de los pliegues), pero sólo en la última década ha habido una mayor atención en la microestructura (longitud de onda de los pliegues). |
|
|
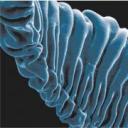
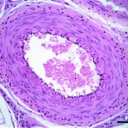
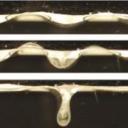
Wrinkling to FoldingUna superficie sobre un sustrato blando formando un recubrimiento tiene la tendencia a formar arrugas periódicas. Esto se observa en casi todas los recubrimientos biológicos debido a una ventaja esencial de este diseño: permite un reservorio de superficie disponible y da extensibilidad. Arterias, venas, esófago, bronquios, etc. cuentan con un plegado del epitelio que tiene esa funcionalidad, además hay diversos ejemplos en la naturaleza de estructuras que necesitan extensibilidad y la logran con este diseño, como el biso o byssus en moluscos. La descripción de este plegado fue dado por Bowden et al. (Nature, 393, 146-149, 1998) y corresponde a una diferencia entre la rigidez del sustrato y la rigidez del recubrimiento. Una inestabilidad que se observa en estos sistemas una vez formada las arrugas es el plegamiento de forma localizada lo que ha sido denominado por nosotros como wrinkling to fold transition. Los pliegues localizados pueden conformar una estructura periódica de diferente naturaleza a la observada en las arrugas y que puede confundirse con una estructura de arrugas. Es de hecho aún una pregunta abierta saber cuánto del plegamiento observado en sistemas biológicos en producto de las arrugas o la acumulación de pliegues localizados. |
|
|
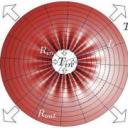
FracturaAl fracturar una superficie por tirar de una lengueta se forman rasgados convergentes que impiden la propagación de la fractura mas allá de una cierta distancia. Esto explica lo dificil que es sacar papel mural de una pared o que al abrir un envase o embalaje se debe repetir el gesto de rasgar muchas veces para poder hacerlo. Esta misma dificultad origina por otra parte el arte del collage llevado a su máxima expresión por Jacques Villeglé: el rasgado da lugar a formas originales como se ilustra en uno de sus cuadros de la columna adjunta. Nosotros hemos investigado las estructuras debido al rasgado tanto en superficies libres como en superficies adheridas a sustratos y estudiado las condiciones para que la convergencia ocurra. Estos estudios nos han permitido formular condiciones para conseguir lo opuesto: rasgados divergentes. El mecanismo permite que el rasgado siga creciendo (en vez de decrecer) lo cual permite que con un gesto un envase o embalaje se pueda abrir con un sólo gesto. La propagación de la fractura en este caso genera rasgados en forma de espiral.
|